Introdução

A cobertura de conjuntos (ou covering design) é uma área da combinatória que estuda como escolher subconjuntos de um conjunto maior de forma que certos critérios de cobertura sejam atendidos. Esses problemas são amplamente aplicados em várias áreas, como sistemas lotéricos, teoria de códigos, design de experimentos, otimização, redes de comunicação e criptografia.

Este artigo explora os conceitos fundamentais de cobertura de conjuntos, o método de construção lexicográfico, o teorema de Schonheim, e exemplos práticos.

Conceitos Básicos

Em termos simples, uma cobertura de conjuntos envolve selecionar subconjuntos de um conjunto maior de forma que todas as combinações possíveis de elementos sejam incluídas em pelo menos um desses subconjuntos. Formalmente, o problema é descrito como , onde:

• v é o número total de elementos no conjunto.
• k é o número de elementos em cada subconjunto.
• t é o tamanho das combinações que devem ser cobertas por pelo menos um subconjunto.

O objetivo é determinar quantos subconjuntos de tamanho k são necessários para cobrir todas as combinações de tamanho t do conjunto original de v elementos.

Exemplo

Considere o problema C(4,3,2), que significa que:

• Temos um conjunto de 4 elementos: {1, 2, 3, 4}.
• Precisamos formar subconjuntos de 3 elementos.
• A condição é que todas as combinações possíveis de 2 elementos (t=2) apareçam em pelo menos um desses subconjuntos.

Os subconjuntos que atendem a essa condição são:

• {1, 2, 3}
• {1, 2, 4}
• {1, 3, 4}

Esses 3 subconjuntos cobrem todas as combinações de 2 elementos: {1, 2}, {1, 3}, {1, 4}, {2, 3}, {2, 4}, {3, 4}. Portanto, C(4,3,2) = 3, pois são necessários 3 subconjuntos para atingir a cobertura.

Método de Construção Lexicográfico

Uma maneira comum de gerar subconjuntos é pelo método lexicográfico ou lex covering, que organiza os subconjuntos de forma sequencial e crescente, de acordo com a ordem dos elementos. Neste método, cada subconjunto é formado escolhendo os elementos em uma ordem crescente, garantindo que cada subconjunto subsequente seja uma combinação “maior” que o anterior em termos lexicográficos.

Exemplo com C(5,3,2)
Para o problema C(5,3,2), que envolve um conjunto {1, 2, 3, 4, 5}, a construção lexicográfica pode gerar os subconjuntos:

• {1, 2, 3}
• {1, 2, 4}
• {1, 2, 5}
• {1, 3, 4}
• {1, 3, 5}
• {1, 4, 5}

Esses subconjuntos são gerados em ordem crescente e garantem que todas as combinações possíveis de 2 elementos sejam cobertas.

Limites Inferiores: Teorema de Schonheim

O número mínimo de subconjuntos necessário para cobrir todas as combinações possíveis de elementos em um problema de cobertura é uma questão central. Um dos teoremas importantes nessa área é o Teorema de Schonheim, que estabelece um limite inferior para o número de subconjuntos necessários.

O Teorema de Schonheim afirma que, para uma cobertura de conjuntos C(v,k,t), o número mínimo de subconjuntos necessários é dado por:

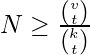
onde é o número de combinações possíveis de t elementos do conjunto de v e é o número de combinações possíveis de t elementos dentro de cada subconjunto de k elementos.

Este limite é útil para determinar se uma solução proposta é eficiente ou se há espaço para otimização.

Aplicação do Teorema de Schonheim

Para C(5,3,2):

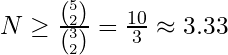
Portanto, são necessários pelo menos 4 subconjuntos para cobrir todas as combinações de 2 elementos em um conjunto de 5 elementos, cada subconjunto contendo 3 elementos.

Aplicações Práticas

A cobertura de conjuntos tem várias aplicações em diferentes campos, incluindo:

1. Sistemas Lotéricos: A otimização de jogos de loteria utiliza cobertura de conjuntos para reduzir o número de apostas necessárias, garantindo que todas as combinações relevantes de números sejam cobertas com o menor número de cartões possível.
2. Teoria de Códigos: Em sistemas de comunicação, garantir que todas as combinações de bits sejam cobertas por códigos corretos minimiza a probabilidade de erro na transmissão de dados.
3. Design de Experimentos: No planejamento de experimentos, subconjuntos são usados para garantir que todas as combinações de fatores sejam testadas, cobrindo todas as interações possíveis entre variáveis.
4. Redes de Comunicação: Em redes, a cobertura de conjuntos é usada para otimizar a transmissão de mensagens, garantindo que todos os nós ou combinações de nós sejam alcançados com o menor número de transmissões.
5. Criptografia: A cobertura de combinações de chaves em sistemas criptográficos aumenta a segurança, garantindo que todas as combinações possíveis sejam cobertas em um conjunto mínimo de operações.

Os problemas de cobertura de conjuntos são centrais na combinatória e possuem diversas aplicações práticas. A construção lexicográfica é um método simples e eficaz para gerar subconjuntos, enquanto o teorema de Schonheim fornece limites teóricos para otimizar a cobertura.

A compreensão desses conceitos permite a solução eficiente de problemas em áreas como redes, design de experimentos e criptografia. O estudo dessas estruturas continua sendo importante para avanços em otimização e segurança computacional.